Расчёты водомётного движителя
Результаты модельных испытаний серий осевых насосов при различных шаговых отношениях H/D или углах поворота лопастей рабочего колеса обычно представляют в форме универсальных диаграмм, связывающих коэффициенты расхода КQ и напора КH с КПД насоса зр , а также с критическим числом кавитации дsкр, при котором начинается срыв напорных характеристик.
На основе оптимизации КПД струи водомета получены следующие соотношения для потребных КH и KQ:
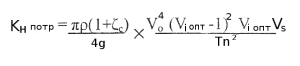
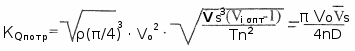
где ρ — 102 кг · с2/м4 и g = 9,81 м/сек2
— массовая плотность воды и ускорение силы тяжести; Т — полная тяга водомета,
кгс; D — диаметр рабочего колеса, м:
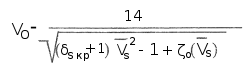
— достижимая скорость движения катера, м/сек:
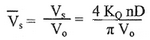
— относительная скорость потока в водозаборнике перед рабочим колесом;
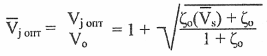
— оптимальное значение относительной скорости струи на срезе, где 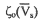 — коэффициент гидравлических
потерь в водозаборной части движителя; ζс = 0,03 — коэффициент потери напора
внутри сопла.
— коэффициент гидравлических
потерь в водозаборной части движителя; ζс = 0,03 — коэффициент потери напора
внутри сопла.
Как уже упоминалось, на быстроходных глиссирующих катерах применяются водозаборники статического типа, входное отверстие которых расположено в плоскости днища (рис. 11).
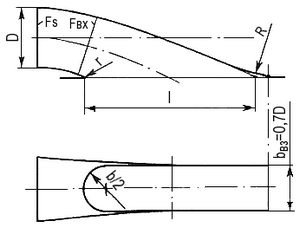
Рис. 11. Основные размеры днищевого водозаборника.
На диаграмме (рис. 12) приведена экспериментальная кривая 1 минимальных значений ζо для водозаборника указанного типа, полученная на основе натурных испытаний серии водозаборников с различными соотношениями геометрических элементов и построенная в зависимости от Vs.
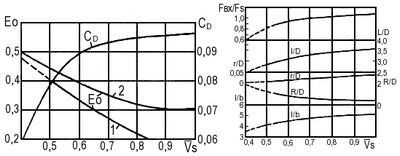
Рис. 12. Зависимости характеристик водозаборника от безразмерной скорости перед рабочим колесом.
Поскольку входное отверстие водозаборника обычно закрывается металлической решеткой из продольных полос, к величине ζомин добавлена относительная потеря напора от установки такой решетки, т. е. суммарный ζо соответствует кривой 2. В этом случае число полос в решетке рассчитывается по формуле
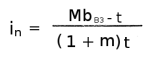
где bвз — ширина входного отверстия водозаборника, мм; t — толщина полосы, мм; m — коэффициент, зависящий от поперечного профиля полосы: m = 0,15 для полос с закругленными по радиусу кромками; m = 0,22 для полос обтекаемого профиля. Ширина полосы обычно принимается не менее пяти ее толщин. Полученное in округляется до целой величины. Оптимальные геометрические соотношения размеров водозаборника, обеспечивающие минимум ζо при каждой Vs, приведены на рис. 11.
Формулы (1) и (2) в комплексе с (3) и кривой формула стр. 29 на рис. 12 б позволяют при заданном δsкр, ограничивающем область оптимальных режимов выбранного насоса, рассчитать и построить диаграмму Tn2 — Vо в осях КHпотр — КQпотр. Совмещение таких диаграмм по осям КH и KQ с универсальными диаграммами ряда типовых насосов позволяет оперативно оценить степень их пригодности в отношении достижимой скорости и развиваемой при этом тяги. На рис. 13 показано совмещение диаграммы Tn2 — Vo, рассчитанной для δsкр = 3, с расходно-напорными характеристиками серии четырехлопастных насосов (описание насосов можно найти в 3 и 5 списка литературы).
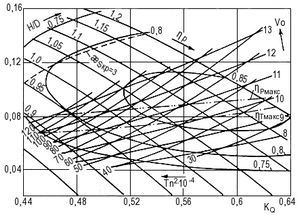
Для учета дополнительных энергетических потерь при использовании геометрически подобных насосов в составе водометов ηр последних снижен на 3 %. Геометрические элементы рабочих колес и спрямляющих аппаратов указанных насосов приведены на рис. 14 и 15.
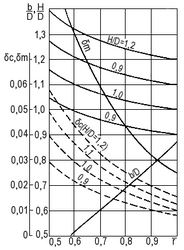
Рис. 14. Геометрические соотношения для четырехлопастных роторов (dст = 0,5; А/Аd = 1/1).
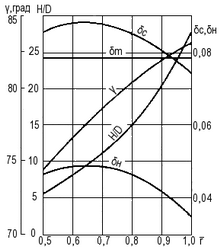
Снимая далее соответствующие значения Tn2, Vo и ηр на каждой линии H/D, можно построить зависимости параметра Тn2 и КПД полной тяги ηт от Vo (см. рис. 16 и 17).
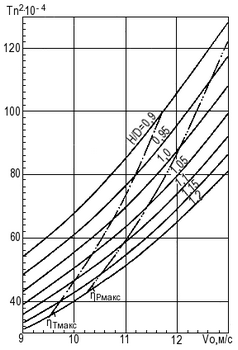
Рис. 16. Зависимость параметра Tn2 от Vo при различных H/D (zрк = 4).
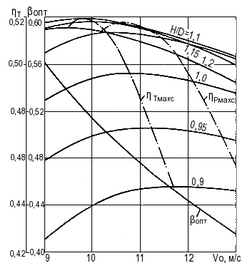
Рис. 17. Зависимость КПД полной тяги ηт от Vo при различных H/D (zрк = 4).
Вычисление ηт производится по формуле
ηт = Т Vо/75N = ηр ηm/(1 + ζc)Vjопт,
где ηт = 0,98 — механический КПД валопровода. В дополнение на рис. 18 нанесена кривая оптимального коэффициента поджатия сопла
βопт = Vs/Vjопт = (dc/D)2,
где dс — диаметр сопла, м.
Кривые ηт характеризуются наличием максимумов, сдвинутых влево относительно линии максимальных КПД самого насоса. Другими словами, на рис. 14 линия оптимальных по ηт режимов работы насоса в составе водомета будет находиться ниже линии максимальных значений ηр. Связь между N и n при каждой Vo можно установить при помощи формулы (7) и данных рис. 16 и 17.
Nn2 = Tn2Vo/75 ηт
Затем из формул (1) и (2) выразить
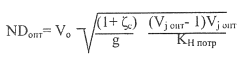
Зависимости проектных параметров Nn2 и nD от Vo при разных H/D рассматриваемой серии насосов представлены на рис. 18 и 19.
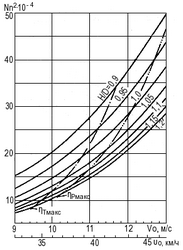
Рис. 18. Взаимосвязь параметра Nn2 c Vo при изменении H/D (zрк = 4).Рис. 19. Изменение параметра nD в зависимости от Vo и H/D (zрк = 4).
При помощи графиков, представленных на рис. 16-19 легко найти оптимальные характеристики водомета с используемым типом насоса при различной форме проектного задания. Расчетную точку желательно расположить на кривой ηтмакс. Отклонение влево от оптимального положения приводит к уменьшению Vo и увеличению Т и наоборот. Видно, что область использования четырехлопастных насосов в оптимальном режиме ограничена диапазоном Vo = 8-13 м/сек (или 29-47 км/час), т. е. они скорее применимы к сравнительно тяжелым и тихоходным катерам.
Для получения более высоких скоростей движения при той же мощности необходимо использовать более высоконапорные насосы с одновременным снижением весовой нагрузки корпуса. На рис. 20 представлена номограмма для определения оптимальных рабочих параметров водомета с высоконапорным шестилопастным насосом, имеющим ротор с поворотными лопастями.

Рис. 20. Номограмма для определения оптимальных параметров водомета с шестилопастным ротором.
Геометрические характеристики этого насоса приведены на рис. 21-23.
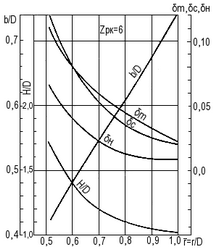
Рис. 21. Геометрические элементы шестилопастного ротора (dст = 0,55; А/Аd = 1,42)
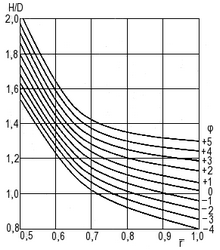
Рис. 22. Зависимость распределения шага вдоль радиуса угла поворота φ
лопастей для шестилопастного ротора.
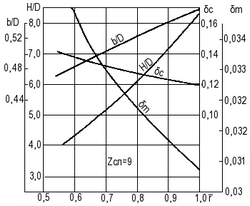
Номограмма соответствует режимам работы насоса по линии ηтмакс; при этом оптимизация диаметра выполнена с учетом зависимости δsкр от φ. Порядок пользования номограммой показан на примере Nn2 = 27 · 104(N = 75 л. с.; n = 3600 об/мин, использован двигатель от автомобиля «ГАЗ-24»). Проведя вертикаль и горизонталь через заданное значение Nn2, получим nD = 11,75; Tn2 = 70 · 104; φ = +2°; Vo = 13,88 м/сек; βопт = 0,2833; Vs = 0,4782. Дополнительно вычисляется Dопт = 0,196 м;T = 194,4 кгс; и через D приведем к размерному виду геометрические элементы ротора и спрямляющего аппарата, пользуясь рис. 23-25.
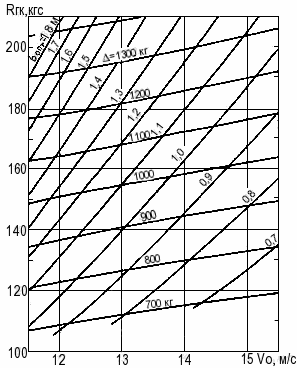
Рис. 24. Расчетная диаграмма оптимальных характеристик глиссирования для корпуса с плоско-килеватым днищем (βк = 15є; хg = 1,8 м).
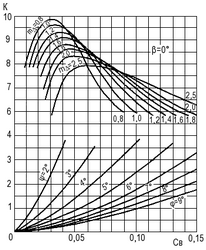
Рис. 25. Зависимость гидродинамического качества (К) от удельной нагрузки и центровки и график для определения ходового дифферента (угла атаки) глиссирующей пластины (β = 0°).
При использовании вместо поворотных лопастей лопастей с фиксированным шагом ротор может оказаться гидродинамически «тяжелым». Это объясняется устранением зазора между корнем лопасти и ступицей. Доводку ротора в этом случае можно осуществить путем подрезки входной и выходной кромок лопастей с последующей их профилировкой.Важно отметить, что при использовании лопаточного поджатая струи желательно иметь четное число спрямляющих лопаток (восемь вместо девяти — рис. 23). Такой переход возможен при сохранении суммарной ширины хорд лопаток zb и их относительной кривизны. Аналогичным образом можно поступить при возникновении технологических трудностей, связанных с изготовлением шестилопастного ротора, когда необходимо увеличить расстояние между корневыми сечениями (например, для выполнения сварки и обработки лопастей). В этом случае число лопастей ротора можно уменьшить до пяти.
Проектируя корпус водометного катера, следует иметь в виду, что установка водомета более предпочтительна на корпусах с плоско-килеватыми обводами днища и постоянным по длине углом килеватости βк = 12-18° (в диапазоне Vo = 40-55 км/час соответственно). Такие обводы обеспечивают более высокую устойчивость на курсе, кроме того, гораздо меньше вероятность прососа воздуха к ротору по сравнению с плоскодонными корпусами. При повышенной килеватости днища центр тяжести двигателя удается расположить гораздо ниже и улучшить заполнение движителя водой при запуске.
Если Т и Vo известны, остается подобрать глиссирующий корпус с допустимой весовой нагрузкой ∆, продольной центровкой xg, углом килеватости βк и оптимальной шириной глиссирования bопт. Сопротивление голого корпуса Rг.к с водометом при глиссировании можно выразить в виде произведения
Rг.к = (T — Ra — RBЗ)(l — ψ), кгс,
в котором
Ra ~ 0,035лобVо2, кгс
— аэродинамическое сопротивление корпуса (Sлоб — наибольшая площадь лобового сечения, м2), кгс;
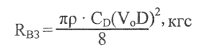
Внешнее гидродинамическое сопротивление водозаборника (CD определяется по рис. 12 после установления Vs), кгс; ψ = 0,02 — коэффициент взаимодействия глиссирующей поверхности с водометом, учитывающий увеличение Rг.к из-за появления дополнительного ходового дифферента, вызванного подсасывающей на днище в районе водозаборного отверстия. Чтобы установить взаимосвязь между Rг.к, Vo, ∆, βк, xg и bопт, можно воспользоваться известными методиками расчета оптимальных характеристик глиссирования. В качестве примера на рис. 24 представлены результаты такого расчета для βк = 15°; xg = 1,8 м и ∆ = 700-1300 кг, объединенные в виде корпусной диаграммы ∆ — bопт в осях Rг.к — Vo.
По диапазону ∆ и Vo эта диаграмма применима для глиссирующих катеров длиной 4,5-5,5 м, оснащенных двигателями N = 50-100 л. с. При помощи такой диаграммы при известных Rг.к, Vo, xg и βк вначале определяются ∆ и bопт, а затем рассчитывается пропульсивный КПД движителя:
η = ηт ηвнеш = ηт{1 — ψ — [RBЗ — (RBЗ + Ra)ψ/T],
где ηвнеш — внешний КПД, выражающий отношение полезной (Rг.к + Rа) и полной тяги Т.






